728x90
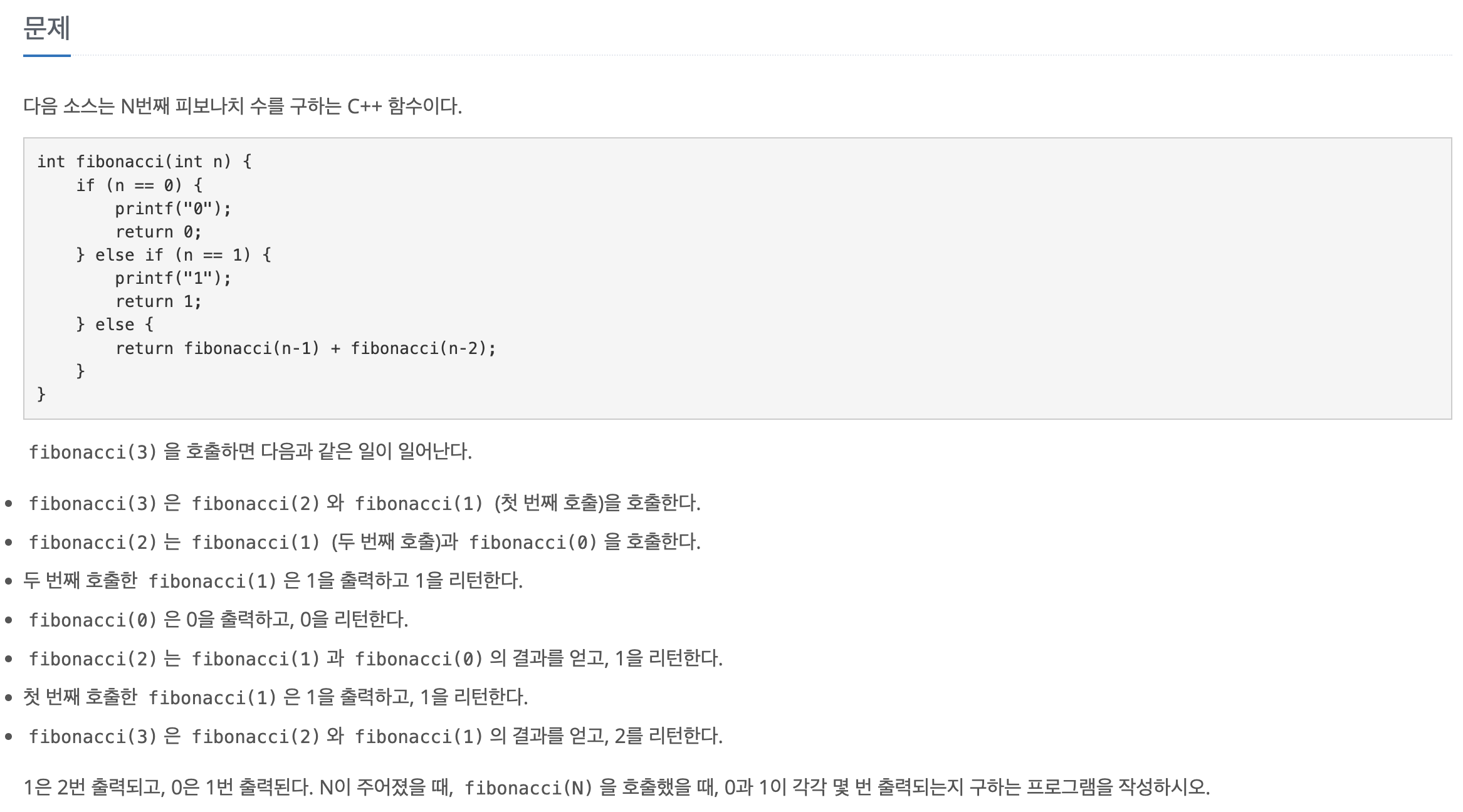
< 문제 >
< 풀이 >
Dynamic Programming
시간복잡도 : O(N)
코드 변수 정의
- dp : 한 번 계산한 값을 저장하여 재사용하기 위한 dp 테이블 생성
def main():
T = int(input())
dp = [(1, 0), (0, 1)] + [(0, 0)] * 39 # N은 최대 40을 갖음 # dp 초기화
# fibo(n-1) + fibo(n-2) 로 0, 1 반환 count 구하는 코드로 구현
for i in range(2, 41):
dp[i] = (dp[i-1][0] + dp[i-2][0], dp[i-1][1] + dp[i-2][1])
for _ in range(T):
N = int(input())
print(dp[N][0], dp[N][1]) # 0이 출력되는 횟수, 1이 출력되는 횟수
if __name__ == "__main__":
main()
풀이 방식
- DP 테이블 초기화
- dp[i] = (zero_cnt, one_cnt) 형식으로 저장한다.
- dp[0] = (1, 0) : fibo(0)을 호출하면 0이 1번 출력, 1이 0번 출력된다.
- dp[1] = (0, 1) : fibo(1)을 호출하면 0이 0번 출력, 1이 1번 출력된다.
- N은 최대 40이므로 dp 테이블의 크기를 40으로 설정한다. ((0, 0)을 39개 추가한다.)
- 점화식
- dp 테이블을 dp[2] ~ dp[40]까지 채운다.
- 미리 테이블 생성 후, N 값에 따라 dp[N] 출력하기 위함.
- 피보나치 성질을 이용하여 dp[i] 값을 갱신한다.
- dp[i][0] = dp[i-1][0] + dp[i-2][0]
- dp[i][1] = dp[i-1][1] + dp[i-2][1]
- fibo(N)을 호출했을 때 fibo(0)과 fibo(1)이 호출된 횟수는 fibo(N-1)과 fibo(N-2)에서 발생한 호출 횟수를 합한 것과 같다.
- dp 테이블을 dp[2] ~ dp[40]까지 채운다.
- 결과 반환
- 2번에서 미리 계산한 dp 테이블에서 N 값을 바로 출력한다.
- return dp[N]
< 회고 >
🤔 💭_
문제를 읽고 dp를 활용해야 할 것 같은 생각을 했지만, 피보나치 수를 구하는 코드를 보고 바로 시도한 바보 같은 풀이가 있었다.

❌ 초기 시도한 코드
def fibo(N, zero_cnt, one_cnt): if N == 0: zero_cnt += 1 return zero_cnt, one_cnt elif N == 1: one_cnt += 1 return zero_cnt, one_cnt else: return fibo(N-1, zero_cnt, one_cnt) + fibo(N-2, zero_cnt, one_cnt) def main(): T = int(input()) for _ in range(T): N = int(input()) cnt = fibo(N, 0, 0) zero_cnt, one_cnt = sum([cnt[i] for i in range(len(cnt)) if i % 2 == 0]), sum([cnt[i] for i in range(len(cnt)) if i % 2 != 0]) print(zero_cnt, one_cnt) if __name__ == "__main__": main()
0~N번째까지의 연산 과정에서 각 fibo(숫자)에서 도출되는 0과 1의 개수를 튜플로 반환하는 무모한 코드를 짰다.
위의 코드를 실행한 결과 예시는 다음과 같다.
T = 1
N = 3
cnt = fibo(3, 0, 0)
print(cnt) # (0, 1, 1, 0, 0, 1) ← 0의 개수 / 1의 개수
짝수 자리의 0의 개수 합과 홀수 자리의 1의 개수 합을 구하여 결과를 출력한다.
제출한 결과 역시나 메모리 초과 문제가 발생하였고, 이 문제는 DP를 활용해서 푸는 게 맞다는 생각으로 다시 풀이를 했다.
우선 dp 테이블에 (0의 개수, 1의 개수)를 저장해야겠다고 생각하고 코드를 구현했다.
N을 입력받을 때마다 dp[N]을 계산해도 되지만, 최대 N이 40까지 밖에 안되니 dp 테이블을 먼저 생성한 후, 입력받은 N에 대해 dp[N]을 출력하는 방식이 조금 더 빠를 것 같다는 생각에 풀이 코드와 같이 구현했다.
728x90
'coding_test > 항해99 코테스터디 TIL' 카테고리의 다른 글
| 99클럽 코테 스터디 _ 23일차 TIL (동적 계획법) (0) | 2025.02.19 |
|---|---|
| 99클럽 코테 스터디 _ 22일차 TIL (동적 계획법, 이분 탐색) (0) | 2025.02.18 |
| 99클럽 코테 스터디 _ 20일차 TIL (우선순위 큐) (0) | 2025.02.14 |
| 99클럽 코테 스터디 _ 19일차 TIL (그리디) (0) | 2025.02.13 |
| 99클럽 코테 스터디 _ 18일차 TIL (우선순위 큐) (0) | 2025.02.12 |
